Auto Grad Functions

Smart Predict-then-Optimize Loss+ (SPO+)

SPO+ [1] is a convex surrogate loss function for SPO Loss (Regret), which measures the decision error of an optimization problem. The objective function is linear with known, fixed constraints, and the cost vector is predicted from contextual data.

class pyepo.func.SPOPlus(optmodel, processes=1, solve_ratio=1, reduction='mean', dataset=None)

An autograd module for SPO+ Loss, as a surrogate loss function of SPO (regret) Loss, which measures the decision error of the optimization problem.

For SPO/SPO+ Loss, the objective function is linear and constraints are known and fixed, but the cost vector needs to be predicted from contextual data.

The SPO+ Loss is convex with subgradient. Thus, it allows us to design an algorithm based on stochastic gradient descent.

Reference: <https://doi.org/10.1287/mnsc.2020.3922>

forward(pred_cost, true_cost, true_sol, true_obj)

Forward pass

pyepo.func.SPOPlus supports parallel computation. The processes parameter sets the number of processors (0 uses all available cores).

import pyepo

spo = pyepo.func.SPOPlus(optmodel, processes=2)

Differentiable Black-box Optimizer (DBB)

DBB [2] estimates gradients via interpolation, replacing the zero gradients of the linear program solver. The objective function is linear with known, fixed constraints, and the cost vector is predicted from contextual data.

class pyepo.func.blackboxOpt(optmodel, lambd=10, processes=1, solve_ratio=1, dataset=None)

An autograd module for differentiable black-box optimizer, which yields an optimal solution and derive a gradient.

For differentiable black-box, the objective function is linear and constraints are known and fixed, but the cost vector needs to be predicted from contextual data.

The black-box approximates the gradient of the optimizer by interpolating the loss function. Thus, it allows us to design an algorithm based on stochastic gradient descent.

Reference: <https://arxiv.org/abs/1912.02175>

forward(pred_cost)

Forward pass

pyepo.func.blackboxOpt supports parallel computation. lambd is a smoothing hyperparameter (recommended range: 10 to 20).

import pyepo

dbb = pyepo.func.blackboxOpt(optmodel, lambd=10, processes=2)

Negative Identity Backpropagation (NID)

NID [6] treats the solver as a negative identity mapping during backpropagation. This is equivalent to DBB with a specific hyperparameter setting. NID is hyperparameter-free and requires no additional solver calls during the backward pass.

class pyepo.func.negativeIdentity(optmodel, processes=1, solve_ratio=1, dataset=None)

An autograd module for the differentiable optimizer, which yields an optimal solution and uses negative identity as a gradient on the backward pass.

For negative identity backpropagation, the objective function is linear and constraints are known and fixed, but the cost vector needs to be predicted from contextual data.

If the interpolation hyperparameter λ aligns with an appropriate step size, then the identity update is equivalent to DBB. However, the identity update does not require an additional call to the solver during the backward pass and tuning an additional hyperparameter λ.

Reference: <https://arxiv.org/abs/2205.15213>

forward(pred_cost)

Forward pass

pyepo.func.negativeIdentity supports parallel computation.

import pyepo

nid = pyepo.func.negativeIdentity(optmodel, processes=2)

Differentiable Perturbed Optimizer (DPO)

DPO [3] uses Monte-Carlo sampling to estimate solutions by optimizing randomly perturbed costs with Gaussian noise. The perturbed optimizer is differentiable with non-zero Jacobian.

class pyepo.func.perturbedOpt(optmodel, n_samples=10, sigma=1.0, processes=1, seed=135, solve_ratio=1, dataset=None)

An autograd module for Fenchel-Young loss using perturbation techniques. The use of the loss improves the algorithm by the specific expression of the gradients of the loss.

For the perturbed optimizer, the cost vector needs to be predicted from contextual data and is perturbed with Gaussian noise.

Thus, it allows us to design an algorithm based on stochastic gradient descent.

Reference: <https://papers.nips.cc/paper/2020/hash/6bb56208f672af0dd65451f869fedfd9-Abstract.html>

forward(pred_cost)

Forward pass

pyepo.func.perturbedOpt supports parallel computation. n_samples is the number of Monte-Carlo samples, and sigma is the Gaussian noise variance.

import pyepo

dpo = pyepo.func.perturbedOpt(optmodel, n_samples=10, sigma=0.5, processes=2)

Perturbed Fenchel-Young Loss (PFYL)

PFYL [3] uses perturbation techniques with Monte-Carlo sampling. By exploiting the specific gradient structure of the Fenchel-Young loss, it directly optimizes a loss between predicted costs and true solutions with less computation than DPO.

class pyepo.func.perturbedFenchelYoung(optmodel, n_samples=10, sigma=1.0, processes=1, seed=135, solve_ratio=1, reduction='mean', dataset=None)

An autograd module for Fenchel-Young loss using perturbation techniques. The use of the loss improves the algorithm by the specific expression of the gradients of the loss.

For the perturbed optimizer, the cost vector needs to be predicted from contextual data and is perturbed with Gaussian noise.

The Fenchel-Young loss allows directly optimizing a loss between the features and solutions with less computation. Thus, it allows us to design an algorithm based on stochastic gradient descent.

Reference: <https://papers.nips.cc/paper/2020/hash/6bb56208f672af0dd65451f869fedfd9-Abstract.html>

forward(pred_cost, true_sol)

Forward pass

pyepo.func.perturbedFenchelYoung supports parallel computation. n_samples is the number of Monte-Carlo samples, and sigma is the Gaussian noise variance.

import pyepo

pfy = pyepo.func.perturbedFenchelYoung(optmodel, n_samples=10, sigma=0.5, processes=2)

Implicit Maximum Likelihood Estimator (I-MLE)

I-MLE [7] uses the perturb-and-MAP framework, sampling noise from a Sum-of-Gamma distribution and interpolating the loss function to approximate finite differences.

class pyepo.func.implicitMLE(optmodel, n_samples=10, sigma=1.0, lambd=10, distribution=None, two_sides=False, processes=1, solve_ratio=1, dataset=None)

An autograd module for Implicit Maximum Likelihood Estimator, which yields an optimal solution in a constrained exponential family distribution via Perturb-and-MAP.

For I-MLE, it works as black-box combinatorial solvers, in which constraints are known and fixed, but the cost vector needs to be predicted from contextual data.

The I-MLE approximates the gradient of the optimizer smoothly. Thus, it allows us to design an algorithm based on stochastic gradient descent.

Reference: <https://proceedings.neurips.cc/paper_files/paper/2021/hash/7a430339c10c642c4b2251756fd1b484-Abstract.html>

forward(pred_cost)

Forward pass

pyepo.func.implicitMLE supports parallel computation.

import pyepo

imle = pyepo.func.implicitMLE(optmodel, n_samples=10, sigma=1.0, lambd=10, processes=2)

Adaptive Implicit Maximum Likelihood Estimator (AI-MLE)

AI-MLE [8] extends I-MLE with an adaptive interpolation step within the perturb-and-MAP framework, sampling noise from a Sum-of-Gamma distribution.

class pyepo.func.adaptiveImplicitMLE(optmodel, n_samples=10, sigma=1.0, distribution=None, two_sides=False, processes=1, solve_ratio=1, dataset=None)

An autograd module for Adaptive Implicit Maximum Likelihood Estimator, which adaptively chooses hyperparameter λ and yields an optimal solution in a constrained exponential family distribution via Perturb-and-MAP.

For AI-MLE, it works as black-box combinatorial solvers, in which constraints are known and fixed, but the cost vector needs to be predicted from contextual data.

The AI-MLE approximates the gradient of the optimizer smoothly. Thus, it allows us to design an algorithm based on stochastic gradient descent.

Reference: <https://ojs.aaai.org/index.php/AAAI/article/view/26103>

forward(pred_cost)

Forward pass

pyepo.func.adaptiveImplicitMLE supports parallel computation.

import pyepo

aimle = pyepo.func.adaptiveImplicitMLE(optmodel, n_samples=10, sigma=1.0, processes=2)

Noise Contrastive Estimation (NCE)

NCE [4] is a surrogate loss based on negative examples. It uses a small set of non-optimal solutions as negative samples to maximize the probability gap between the optimal solution and the rest.

class pyepo.func.NCE(optmodel, processes=1, solve_ratio=1, reduction='mean', dataset=None)

An autograd module for noise contrastive estimation as surrogate loss functions, based on viewing suboptimal solutions as negative examples.

For the NCE, the cost vector needs to be predicted from contextual data and maximizes the separation of the probability of the optimal solution.

This allows us to design an algorithm based on stochastic gradient descent.

Reference: <https://www.ijcai.org/proceedings/2021/390>

forward(pred_cost, true_sol)

Forward pass

pyepo.func.NCE supports parallel computation (0 uses all available cores).

import pyepo

nce = pyepo.func.NCE(optmodel, processes=2, solve_ratio=0.05, dataset=dataset)

Contrastive Maximum A Posteriori Estimation (CMAP)

CMAP [4] is a special case of NCE that uses only the single best negative sample. It is simpler and often equally effective.

class pyepo.func.contrastiveMAP(optmodel, processes=1, solve_ratio=1, reduction='mean', dataset=None)

An autograd module for Maximum A Posterior contrastive estimation as surrogate loss functions, which is an efficient self-contrastive algorithm.

For the MAP, the cost vector needs to be predicted from contextual data and maximizes the separation of the probability of the optimal solution.

Thus, it allows us to design an algorithm based on stochastic gradient descent.

Reference: <https://www.ijcai.org/proceedings/2021/390>

forward(pred_cost, true_sol)

Forward pass

pyepo.func.contrastiveMAP supports parallel computation (0 uses all available cores).

import pyepo

cmap = pyepo.func.contrastiveMAP(optmodel, processes=2, solve_ratio=0.05, dataset=dataset)

Learning to Rank (LTR)

LTR [5] learns an objective function that correctly ranks a pool of feasible solutions. LTR methods assign scores to solutions and define surrogate losses that encourage ranking the optimal solution highest.

Pointwise loss computes ranking scores for individual solutions.

class pyepo.func.pointwiseLTR(optmodel, processes=1, solve_ratio=1, reduction='mean', dataset=None)

An autograd module for pointwise learning to rank, where the goal is to learn an objective function that ranks a pool of feasible solutions correctly.

For the pointwise LTR, the cost vector needs to be predicted from contextual data, and calculates the ranking scores of the items.

Thus, it allows us to design an algorithm based on stochastic gradient descent.

Reference: <https://proceedings.mlr.press/v162/mandi22a.html>

forward(pred_cost, true_cost)

Forward pass

Pairwise loss learns the relative ordering between pairs of solutions.

class pyepo.func.pairwiseLTR(optmodel, processes=1, solve_ratio=1, reduction='mean', dataset=None)

An autograd module for pairwise learning to rank, where the goal is to learn an objective function that ranks a pool of feasible solutions correctly.

For the pairwise LTR, the cost vector needs to be predicted from the contextual data and the loss learns the relative ordering of pairs of items.

Thus, it allows us to design an algorithm based on stochastic gradient descent.

Reference: <https://proceedings.mlr.press/v162/mandi22a.html>

forward(pred_cost, true_cost)

Forward pass

Listwise loss evaluates scores over the entire ranked list.

class pyepo.func.listwiseLTR(optmodel, processes=1, solve_ratio=1, reduction='mean', dataset=None)

An autograd module for listwise learning to rank, where the goal is to learn an objective function that ranks a pool of feasible solutions correctly.

For the listwise LTR, the cost vector needs to be predicted from the contextual data and the loss measures the scores of the whole ranked lists.

Thus, it allows us to design an algorithm based on stochastic gradient descent.

Reference: <https://proceedings.mlr.press/v162/mandi22a.html>

forward(pred_cost, true_cost)

Forward pass

All three variants support parallel computation (0 uses all available cores).

import pyepo

# pointwise
ltr = pyepo.func.pointwiseLTR(optmodel, processes=2, solve_ratio=0.05, dataset=dataset)
# pairwise
ltr = pyepo.func.pairwiseLTR(optmodel, processes=2, solve_ratio=0.05, dataset=dataset)
# listwise
ltr = pyepo.func.listwiseLTR(optmodel, processes=2, solve_ratio=0.05, dataset=dataset)

Perturbation Gradient (PG)

PG [9] is a surrogate loss based on zeroth-order gradient approximation via Danskin’s Theorem. It uses finite differences along the true cost direction to estimate informative gradients through the optimization solver.

class pyepo.func.perturbationGradient(optmodel, sigma=0.1, two_sides=False, processes=1, solve_ratio=1, reduction='mean', dataset=None)

An autograd module for PG Loss, as a surrogate loss function of objective value, which measures the decision quality of the optimization problem.

For PG Loss, the objective function is linear, and constraints are known and fixed, but the cost vector needs to be predicted from contextual data.

According to Danskin’s Theorem, the PG Loss is derived from different zeroth order approximations and has the informative gradient. Thus, it allows us to design an algorithm based on stochastic gradient descent.

Reference: <https://arxiv.org/abs/2402.03256>

forward(pred_cost, true_cost)

Forward pass

pyepo.func.perturbationGradient supports parallel computation (0 uses all available cores). sigma controls the finite difference width. two_sides enables central differencing for more accurate gradient estimates.

import pyepo

pg = pyepo.func.perturbationGradient(optmodel, sigma=0.1, two_sides=False, processes=2)

Parallel Computation

All pyepo.func modules support parallel solving during training via the processes parameter.

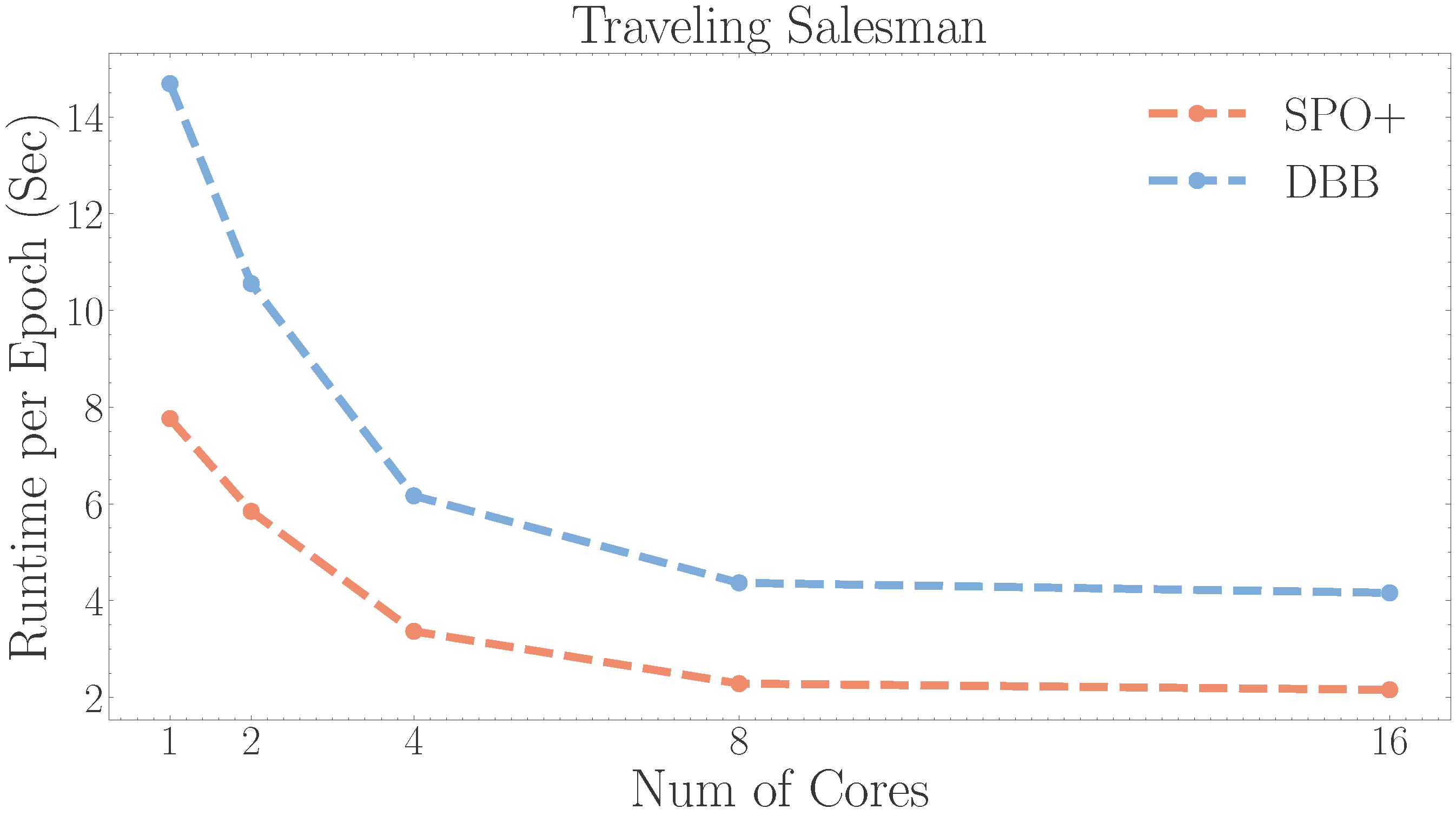
The figure shows that increasing the number of processes reduces runtime.

Footnotes

[1]

Elmachtoub, A. N., & Grigas, P. (2021). Smart “predict, then optimize”. Management Science.

[2]

Vlastelica, M., Paulus, A., Musil, V., Martius, G., & Rolínek, M. (2019). Differentiation of blackbox combinatorial solvers. arXiv preprint arXiv:1912.02175.

[3] (1,2)

Berthet, Q., Blondel, M., Teboul, O., Cuturi, M., Vert, J. P., & Bach, F. (2020). Learning with differentiable perturbed optimizers. Advances in neural information processing systems, 33, 9508-9519.

[4] (1,2)

Mulamba, M., Mandi, J., Diligenti, M., Lombardi, M., Bucarey, V., & Guns, T. (2021). Contrastive losses and solution caching for predict-and-optimize. Proceedings of the Thirtieth International Joint Conference on Artificial Intelligence.

[5]

Mandi, J., Bucarey, V., Mulamba, M., & Guns, T. (2022). Decision-focused learning: through the lens of learning to rank. Proceedings of the 39th International Conference on Machine Learning.

[6]

Sahoo, S. S., Paulus, A., Vlastelica, M., Musil, V., Kuleshov, V., & Martius, G. (2022). Backpropagation through combinatorial algorithms: Identity with projection works. arXiv preprint arXiv:2205.15213.

[7]

Niepert, M., Minervini, P., & Franceschi, L. (2021). Implicit MLE: backpropagating through discrete exponential family distributions. Advances in Neural Information Processing Systems, 34, 14567-14579.

[8]

Minervini, P., Franceschi, L., & Niepert, M. (2023, June). Adaptive perturbation-based gradient estimation for discrete latent variable models. In Proceedings of the AAAI Conference on Artificial Intelligence (Vol. 37, No. 8, pp. 9200-9208).

[9]

Gupta, V., & Huang, M. (2024). Decision-Focused Learning with Directional Gradients. arXiv preprint arXiv:2402.03256.